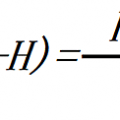1-8.Why is the constant drying period. – Moisture movement in wet material.

INDEX

Fick’s first law
Fick’s second law
- ★ Case Study: When drying moisture material as high initial moisture content with The Air Blow Heater.

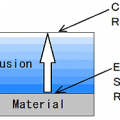
Inside moisture material, movement of water (liquid) mainly takes place from the point that moisture content is high to a low point on the surface from an inside in accordance with a slope.

There is capillary suction force action, osmotic suction force action.
The thing of such a movement is called “Diffusion.”

The Diffusion is a physical phenomenon which particles, heat, quantity of motion, etc. are scattered spontaneously, and spreads.
The Diffusion is a kind of transport phenomena and a diffusion equation can define it.
For example, the diffusion of macroscopic molecule follows Fick’s law.
The Diffusion of macroscopic thermal energy follows the law of Fourier’s heat conduction.
In any case, it can see the obvious diffusion only when there is a gradient in the field of physical quantities.
For example, in the thermal diffusion, since heat moves at the same speed as one way and its opposite direction when temperature is constant, it is not changeful as the whole.

These flux densities equal in the value that took the coefficient indicating the physical property for the gradient .

The flux densities :each molecules, energy, electronic flow
The coefficient :the diffusion coefficient, thermal conductivity, electrical conductivity
The gradient :concentration gradient, temperature incline, electric potential gradient (electric field)

<<Adolf Eugen Fick (3 September 1829 – 21 August 1901) German physician and physiologist>>

Fick’s first law

Fick’s first law relates the diffusive flux to the concentration under the assumption of steady state. It postulates that the flux goes from regions of high concentration to regions of low concentration, with a magnitude that is proportional to the concentration gradient (spatial derivative). In one (spatial) dimension, the law is

J is the "diffusion flux" [(amount of substance) per unit area per unit time], D is the diffusion coefficient or diffusivity in dimensions of [length2 time−1], Φ (for ideal mixtures) is the concentration in dimensions of [amount of substance per unit volume], x is the position [length]

D is proportional to the squared velocity of the diffusing particles, which depends on the temperature, viscosity of the fluid and the size of the particles according to the Stokes-Einstein relation. In dilute aqueous solutions the diffusion coefficients of most ions are similar and have values that at room temperature are in the range of 0.6×10−9 to 2×10−9 m2/s. For biological molecules the diffusion coefficients normally range from 10−11 to 10−10 m2/s.
In two or more dimensions we must use ∇, the del or gradient operator, which generalises the first derivative, obtaining

The driving force for the one-dimensional diffusion is the quantity
.

which for ideal mixtures is the concentration gradient. In chemical systems other than ideal solutions or mixtures, the driving force for diffusion of each species is the gradient of chemical potential of this species. Then Fick’s first law (one-dimensional case) can be written as:

where the index i denotes the ith species, c is the concentration (mol/m3), R is the universal gas constant (J/(K mol)), T is the absolute temperature (K), and μ is the chemical potential (J/mol).
If the primary variable is mass fraction (yi), then the equation changes to:

where p is the fluid density. Note that the density is outside the gradient operator.

Fick’s second law

Fick’s second law predicts how diffusion causes the concentration to change with time:

Φ is the concentration in dimensions of [(amount of substance) length−3], t is time [s] D is the diffusion coefficient in dimensions of [length2 time−1], x is the position [length]

<<Jean Baptiste Joseph Fourier, Baron de、 (21 March 1768 – 16 May 1830) French mathematician and physicist>>

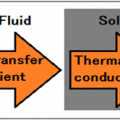
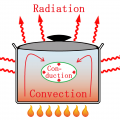
Heat conduction (or thermal conduction) is the transfer of internal energy by microscopic diffusion and collisions of particles or quasi-particles within a body due to a temperature gradient. The microscopically diffusing and colliding objects include molecules, electrons, atoms, and phonons. They transfer disorganized microscopic kinetic and potential energy, which are jointly known as internal energy. Conduction can only take place within an object or material, or between two objects that are in direct or indirect contact with each other. Conduction takes place in all forms of ponderable matter, such as solids, liquids, gases and plasmas.

Whether by conduction or by thermal radiation, heat spontaneously flows from a hotter to a colder body. In the absence of external drivers, temperature differences decay over time, and the bodies approach thermal equilibrium.

In conduction, the heat flow is within and through the body itself. In contrast, in heat transfer by thermal radiation, the transfer is often between bodies, which can be spatially separate. Also possible is transfer of heat by a combination of conduction and thermal radiation. In convection, internal energy is carried between bodies by a material carrier. In solids, conduction is mediated by the combination of vibrations and collisions of molecules, of propagation and collisions of phonons, and of diffusion and collisions of free electrons. In gases and liquids, conduction is due to the collisions and diffusion of molecules during their random motion. Photons in this context do not collide with one another, and so heat transport by electromagnetic radiation is conceptually distinct from heat conduction by microscopic diffusion and collisions of material particles and phonons. In condensed matter, such as a solid or liquid, the distinction between conduction and radiative transfer of heat is clear in physical concept, but it is often not phenomenologically clear, unless the material is semi-transparent. In a gas the distinction is both conceptually and phenomenologically clear.

In the engineering sciences, heat transfer includes the processes of thermal radiation, convection, and sometimes mass transfer. Usually more than one of these processes occurs in a given situation. The conventional symbol for the material property, thermal conductivity, is k.

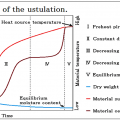
★ Case Study: When drying moisture material as high initial moisture content with The Air Blow Heater.

The water near the surface is evaporated by the hot air .
The water is diffused from the inside to the surface , near the surface keeps the wet at all times .
A part of thermal energy of the hot air is consumed as evaporative latent heat on the surface.
The amount of evaporation of water increases as material temperature increases .
Therefore, as the material temperature increases , consumption of thermal energy also increases .
Temperature will be kept constant when the thermal energy supplied to material from the Air Blow Heater and the thermal energy consumed as evaporative latent heat balance.
Material temperature is kept constant , the amount of evaporation is constant , the drying speed will also be constant.
This state is called the constant drying speed.
The period which this constant drying speed is continuing is called the constant drying rate period.
Therefore if there is that thermal energy consumption and thermal energy supply is not balanced, it does not appear the constant drying speed and the constant drying rate period.

* Latent heat

Latent heat is the energy released or absorbed by a body or a thermodynamic system during a constant-temperature process.
A typical example is a change of state of matter, meaning a phase transition such as the melting of ice or the boiling of water.
The term was introduced around 1762 by Scottish chemist Joseph Black. It is derived from the Latin latere (to lie hidden).
Black used the term in the context of calorimetry when referring to the heat transferred that caused a change of volume while the thermodynamic system was held at constant temperature.
In contrast to latent heat, an energy is called a sensible energy or heat when it causes processes that do result in a change of the temperature of the system.