An object with an absolute temperature of 0K (Kelvin) or higher radiates a wavelength corresponding to the temperature of the object as an electromagnetic wave. The object that received this electromagnetic wave has received heat. This transfer of heat is called heat radiation. The heat radiation of an object varies greatly depending on the plane temperature and plane condition.
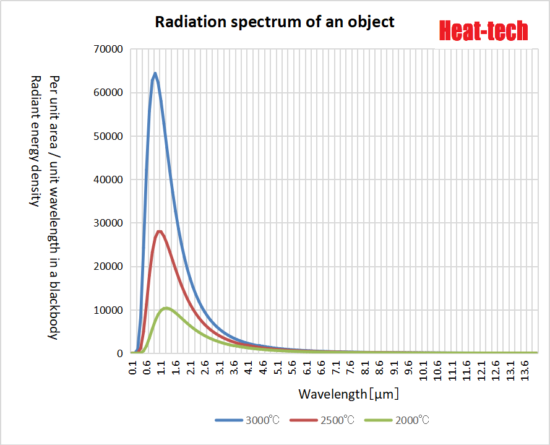
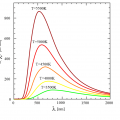
According to Planck’s law, the energy radiated by heat draws a parabolic line that is convex upward with the maximum wavelength at the apex, and radiates a wide range of electromagnetic waves from short wavelengths to long wavelengths. The higher the temperature, the higher the radiant energy density of each wavelength.
In the above figure, the radiant energy density W (λ, T) per unit area and unit wavelength in a blackbody is calculated from the following formula.
W (λ, T) = 8πhc / λ5 / (exp (hc / λkT) -1) [w / m2]
Λ: Wavelength [m] h: Planck’s constant 6.626 × 10 ^ -34 [J ・ s] c: Speed of light 3 × 10 ^ 8 [m / s]
K: Boltzmann constant 1.3807 × 10 ^ -23 [J / K] T: Blackbody temperature [K]
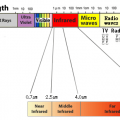
The maximum wavelength of heat radiation is inversely proportional to the temperature of the heating element. Considering the heating element temperature of the heater, if the heating element temperature is high, it emits electromagnetic waves (light) with the maximum wavelength in the near-infrared region, and if it is high, it emits electromagnetic waves (light) with the maximum wavelength in the far-infrared region. Of these electromagnetic waves, heat radiation is in the range of λ0.4 μm (visible light) to 100 μm (far infrared rays).
Maximum wavelength of heat radiation λmaxT = 2.90 × 10 ^ -3 / T (K) m Wien’s displacement law
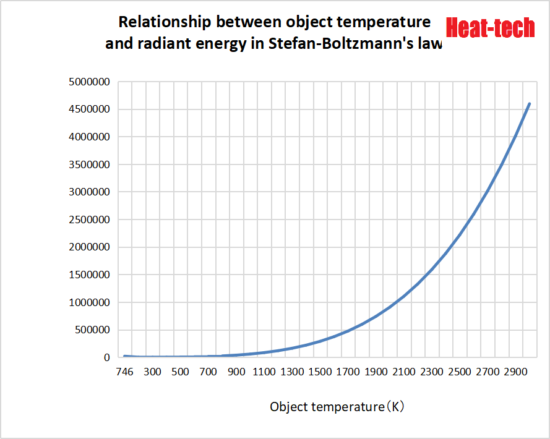
The radiant energy of a blackbody at temperature T is expressed below by Stefan-Boltzmann’s law.
Eb = σ (Stefan-Boltzmann constant: 5.67 × 10 ^ -8) × T (object temperature) ^ 4 [W / m2]
Since radiant energy is proportional to the fourth power of absolute temperature, it changes significantly with respect to temperature even when compared to heating by convection or heat conduction. If the object temperature is about normal temperature, the energy from radiation can be ignored, but the higher the temperature, the greater the difference and the more advantageous the heating by radiation.
Eb = 5.67 × 10 ^ -8 × T ^ 4 [W / m2] holds when the surroundings are at absolute zero (0K).
In this formula, the ambient temperature is 0K and there is no difference, so it is omitted as “object temperature-ambient temperature (0K)”. If user enter 0K, the formula will be as follows.
“Eb = 5.67 × 10 ^ -8 × (T (object temperature) -T (ambient temperature (0K)) ^ 4) [W / m2]
Therefore, the actual energy radiation density is four times the value obtained by subtracting the ambient temperature from the object temperature.
 HEAT-TECH Best Technology Online Shop
HEAT-TECH Best Technology Online Shop