절대 온도가 0K(켈빈) 이상의 물체는 물체의 온도에 따른 파장을 전자파로서 방사합니다. 이 전자파를 받은 물체는 열을 받게 됩니다. 이 열의 이동을 열방사라고 합니다. 물체의 열방사는 표면온도나 표면상태에 따라 크게 변
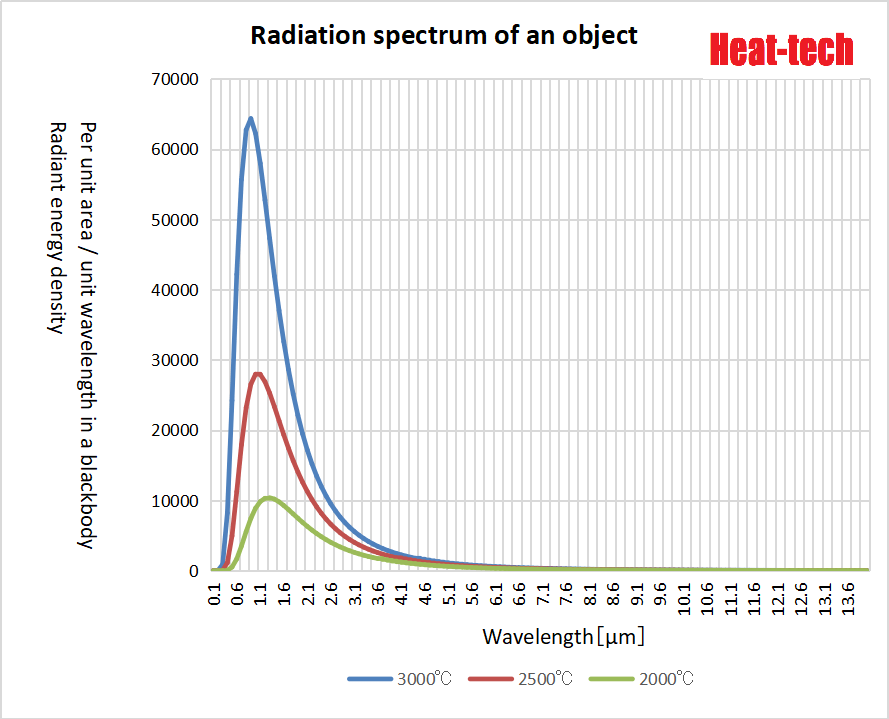
열방사되는 에너지는 플랑크의 법칙과 같이 최대파장을 정점으로 위로 볼록한 포물선을 그려 단파장에서 장파장까지 폭넓게 전자파를 방사하고 있습니다. 온도가 높을수록 각 파장의 방사 에너지 밀도가 높아집니다.

위의 그림은 흑체에 있어서의 단위 면적·단위 파장당의 방사 에너지 밀도 W(λ, T)를 아래의 식으로부터 구하고 있습니다.

　W(λ,T) = 8πhc/λ5/( exp( hc/λkT ) -1)～[w/m2]
～λ：파장［m］h：플랑크 정수 6.626×10^-34[J・s］　c：광속 3×10^8[m/s]
～k：볼츠만 정수 1.3807×10^-23　[J/K] T：흑체 온도[K]

열 방사선의 최대 파장은 발열체의 온도에 반비례합니다. 히터의 발열체 온도에서 생각하면, 발열체 온도가 높으면 근적외선 영역에, 높으면 원적외선 영역에 최대 파장을 가지는 전자파(광)를 방사합니다. 이 전자파 중 열방사는 λ0.4μm(가시광)~100μm(원적외선) 정도의 범위입니다.

열방사의 최대 파장 λmaxT= 2.90×10^-3/T(K) m 빈의 변위칙

온도 T의 흑체의 방사 에너지는 스테판 볼츠만의 법칙에 의해 아래와 같이 나타납니다.
Eb=σ(스테판 볼츠만 정수:5.67×10^-8) ×T(물체 온도)^4[W/m2]
방사 에너지는 절대 온도의 4승에 비례하기 때문에 대류나 열전도에 의한 가열과 비교해도 온도에 관하서 크게 변화합니다. 물체 온도가 상온 정도이면 방사에 의한 에너지는 무시할 수 있지만, 방사에 고온이 될수록 그 차이는 커지고 방사에 의한 가열이 유리해집니다.

Eb=5.67×10^-8 ×T^4[W/m2]는 주위가 절대 영도(0K)일 때에 성립합니다.
이 식에서는 주위온도가 0K로 차이가 없기 때문에 「물체온도-주위온도(0K)」가 되어 생략됩니다. 0K를 넣으면 아래와 같은 식이 됩니다.
Eb=5.67×10^-8 ×(T(물체의 온도)-T(주위 온도(0K))^4)[W/m2]
그 때문에, 물체 온도로부터 주위 온도를 감산한 수치의 4배가 실제의 에너지 방사 밀도입니다.

【참고】흑체(코쿠타이, black body)란, 외부로부터 입사하는 전자파를, 모든 파장에 걸쳐 완전하게 흡수하고, 또한 열방사할 수 있는 이상적 물체입니다. 흑체는 실재하지 않지만 자연과학을 설명하는데 있어서 자주 등장하는 중요한 모델입니다.