INDEX
열역학 제0법칙 – 열평형의 법칙

제임스・클러크・맥스웰 (James Clerk Maxwell, 1831 년 6 월 13 일 – 1879 년 11 월 5 일) 영국의 이론 물리학
열역학의 체계가 완성 된 후 맥스웰이 기본 법칙 중 하나로 꼽았다.
물체 A와 B, B와 C가 각각 열 평형이라면 A와 C도 열 평형에있는
AT=BT, BT=CT ⇒ AT=CT
수학적 추이 율이 성립됩니다
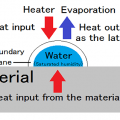
열 평형 = 열역학 평형은 열역학적 계가 열, 화학적, 역학적으로 평형 인 것을 말한다.
즉, 물질과 에너지 (열)의 순 흐름이없고, 상전이 (얼음에서 물로 변화 등)도 일어나지 않은 상태이다.
계가 열역학적 평형 상태에있는 경우 계를 외계로부터 고립시켜 변화는 생기지 않는다.
열역학 제1법칙 – (에너지 보존의 법칙)

제임스・프레스콧・줄 (James Prescott Joule, 1818 년 12 월 24 일 – 1889 년 10 월 11 일)은 영국의 물리학자.

율리우스・로베르트・폰・마이어 (Julius Robert von Mayer, 1814 년 11 월 25 일 – 1878 년 3 월 20 일)는 독일의 물리학자.
줄과 폰・ 마이어는 동시대에 개별적으로 에너지 보존 법칙 (열역학 제 1 법칙)을 발견했다고되어 있습니다.
「계에 ΔQ 만 열을 가하면 외부에 ΔW의 직장을하고 나머지는 내부 에너지 ΔU로 축적한다.」
ΔQ=ΔW+ΔU
ΔQ:계에 주어진 열량
ΔW:계에서 꺼내 진 직장
ΔU:계의 내부 에너지 U의 증가량
열역학 제2법칙 – (불가역성의 법칙)

루돌프・줄리어스・엠마뉴엘・쿠라우지우스 (Rudolf Julius Emmanuel Clausius 1822 년 1 월 2 일 – 1888 년 8 월 24 일)는 독일의 물리학자
1854 년 논문 「역학적 열 이론의 두 번째 기본 정리 한 개량형 정보 」를 발표했다. 열역학 제 2 법칙을 확립시켰다.
「열은 항상 온도 차이를 없애는 경향을 나타내고 따라서 항상 고온 물체에서 저온 물체로 이동한다.」
![]()
Q:직장에서 발생한 열량
T:온도
열역학 제3법칙 – 절대0℃에서 엔트로피는 0가된다.

발터・헤르만・네른스트 (Walther Hermann Nernst 1864 년 6 월 25 일 – 1941 년 11 월 18 일)는 독일의 화학자, 물리화학자.
1906 년에 논문으로 발표 1920 년 열역학 제 3 법칙의 공적으로 노벨 화학상을 수상
절대0℃에서 엔트로피는 0가된다.
![]()
푸리에의 법칙 – 열전도 방정식 – 열유속 밀도는 온도 구배에 비례한다

장・바티스트・조제프・푸리에 남작 (Jean Baptiste Joseph Fourier, Baron de 1768 년 3 월 21 일 – 1830 년 5 월 16 일)는 프랑스의 수학자 · 물리학자.
1812년, 논문 「열의 해석적 이론」을 제출해 아카데미 대상을 수상
1822년, 저서 『열의 해석적 이론(Theorie Analytique de la Chaleur)』을 출판
단위 시간에 단위 면적을 흐르는 열 흐름 (열유속 밀도)를 J [W / m2]로 온도를 T라고하면 분자 론적 열 완화 시간보다 충분히 긴 시간 (정상 상태라고 볼 시간) 영역에서의 현상 대해 열유속가 밀도 J는 온도 구배 grad T에 비례한다.
![]()
J [W/m2] : 열 흐름 (열유속 밀도)
λ: 열전도율
grad T : 온도 구배
T : 온도
물질이 등방 적이면 λ는 스칼라로 표현됩니다.
일반적으로 비 등방성으로 3 차원 계에서는 J와 grad T의 방향은 일치하지 않고 열전도율은 텐서로 표현됩니다.
픽의 확산 법칙 – 확산 유속은 농도 구배에 비례

아돌프・오이겐・픽 (Adolf Eugen Fick 1829 년 9 월 3 일 – 1901 년 8 월 21 일)는 독일의 생리학자, 물리학자, 의사
픽의 확산 법칙은 1855 년에 발표 된 제1법칙과 제2법칙이 있습니다.
제1법칙은 정상 상태 확산, 즉 확산에 의한 농도가 시간에 대해 변하지 않을 때 사용되며 「확산 유속은 농도 구배에 비례한다」는 법칙입니다. 공업적인 정상 상태 확산은 수소 가스의 순화에 볼 수 있습니다.
J=-D grad c
J는 확산 뭉치 또는 유속 (flux)라고하며, 단위 시간당 단위 면적을 통과 한 성격의 양으로 정의된다. 질량이 통과하는 경우에는 차원은 [ML-2T-1]로 주어집니다.
D는 확산 계수 (diffusion coefficient) 차원은 [L2T-1]c는 농도에서 차원은 [ML-3]
제2법칙은 비정상 상태 확산, 즉 확산의 농도가 시간에 대하여 변경 될 때 사용됩니다. 보통의 확산은 비정상 상태입니다. 확산 계수 D가 상수 일 때 농도 c의 시간 변화는 다음의 확산 방정식으로 표현됩니다 :
![]()
J는 확산 뭉치 또는 유속 (flux)라고하며, 단위 시간당 단위 면적을 통과 한 성격의 양으로 정의된다. 질량이 통과하는 경우에는 차원은 [ML-2T-1]로 주어집니다.
D는 확산 계수 (diffusion coefficient) 차원은 [L2T-1]c는 농도에서 차원은 [ML-3]
줄의 법칙

제임스・프레스콧・줄 (James Prescott Joule, 1818 년 12 월 24 일 – 1889 년 10 월 11 일)은 영국의 물리학자.
줄의 법칙(Joule’s law)은 열역학제1법칙의 발견자 제임스·프레스 코트·줄에 의해 발견되어, 1840년 영국 왕립협회에 발표, 게다가 상세한 논문을 피로소피카루·매거진지에 발표되었습니다.
줄의 제1법칙은 도체를 흐르는 전류와, 전류에 의해 만들어 내지는 열의 관계를 나타낸 법칙입니다.
![]()
Q:만들어 내지는 열량(J)
I:전류값(A)
R:저항치(Ω)
t:전류가 통함 시간(s)
줄의 제2법칙은, 이상 기체의 내부에너지는 그 압력이나 체적에는 의존하지 않고, 온도에만 의존한다고 하는 법칙입니다.
![]()
U:이상 기체의 내부에너지
T:이상 기체의 온도
f:이상 기체 에너지 함수
보일·샤를의 법칙

로버트·보일(Robert Boyle, 1627년1월25일-1691년12월 30일)은 아일랜드·리즈모아의 귀족, 자연 철학자, 화학자, 물리학자, 발명가.

잭·알렉산드르·세자르·샤를(Jacques Alexandre Cesar Charles, 1746년11월12일-1823년4월 7일)은 프랑스의 발명가, 물리학자, 수학자, 기구 탐(탈 것).

조셉·루이·게이=류삿쿠(Joseph Louis Gay-Lussac, 1778년12월6일-1850년5월 9일)은, 프랑스의 화학자, 물리학자
보일·샤를의 법칙은, 이상 기체의 체적와 압력과 온도에 관계되는 법칙.
로버트·보일이 발견한 보일의 법칙과, 잭·샤를이 발견한 샤를의 법칙을 조합시킨 것입니다.
보일의 법칙은 1660년 보일이 발견.
샤를의 법칙은, 1787년에 잭·샤를이 발견하고, 1802년에 조셉·루이·게이=류삿쿠에 의해 처음으로 발표되었습니다.
「기체의 압력P 은 체적V 에 반비례해 절대온도T 에 비례한다」
![]()
![]()
V∝T
V=Vo(1+t/237.15)
K : 절대 온도 -273.15 ℃
0 ℃의 이상 기체는 273 ℃에서 2 배로 팽창합니다.
25 ℃의 이상 기체는 298 ℃에서 2 배로 팽창합니다.
아보가드로의 법칙(Avogadro’s law)

로렌쯔·로마노·아메데오·칼러·아보가도로、쿠아레냐와 뽀뽀 렛의 백작(Lorenzo Romano Amedeo Carlo Avogadro, conte di Quaregna e Cerreto, 1776년8월9일-1856년7월 9일)은, 사르데냐(Sardegna)왕국 (현:이탈리아)토리노 출신의 물리학자, 화학자.
모든 이상 기체에 1kmol의 체적는, 표준상태에 있어서, 동일한 체적, V=22.413m3을 가진다.
(표준상태:P=1.01325xHPa T=273.15K ≒0℃/1atm)
뉴턴의 냉각 법칙

아이색·뉴턴(Isaac Newton, 1642년12월25일-1727년3월 20일)은, 잉글랜드의 물리학자, 자연 철학자, 수학자
액체나 기체 등의 매질중에 두어진 고온의 고체가 매질에 의해 냉각되는 모양을 나타낸 법칙입니다.
이 법칙은 경험적으로 이끌어진 법칙이므로 매질과 고체와의 온도차이가 극단적으로 클 경우에는 성립되지 않을 것도 있습니다만, 일상적인 범위에서 충분히 실용입니다.
매질중의 고체부터 매질로 열이 전해지는 속도는, 고체의 표면적 및 고체와 매질의 온도차이에 비례합니다.
고체가 가지는 열량Q ,시각t ,고체의 표면적S ,고체의 온도T ,매질의 온도Tm 의 사이에는 다음 관계가 성립합니다.
![]()
여기서 비례 상수α은 고체의 표면, 매질의 성질 및 흐르는 방법등에 의해 결정되는 상수로, 열전달율 또는 표면열전도율이라고 합니다.
 HEAT-TECH 최선의 기술 온라인(on-line) 샵
HEAT-TECH 최선의 기술 온라인(on-line) 샵